An analysis earlier this year of more than 100 studies of math interventions finds that students who study already-worked example problems improved in mathematics nearly a half of a standard deviation more than those who didn’t use that approach. That improvement is like a student who would normally score at the 50th percentile performing above the 69th percentile instead.
For students who have gaps in prior math knowledge, the study review suggests that analyzing both correctly and incorrectly answered examples might improve their understanding. But the study found that students tend to make less progress with problems that lack detail, don’t clarify the goal of the problem, or don’t try to highlight the upcoming steps needed to solve the problem.
Julie Booth, an education professor at Temple University, and Allie Huyghe, an assistant director at the Strategic Education Research Partnership Institute, a nonprofit group that develops research-based education practices, have created free example-based lessons in elementary math and algebra. They are now working with California and Maryland teachers in schools serving high percentages of low-income students and students of color to do the same in geometry.
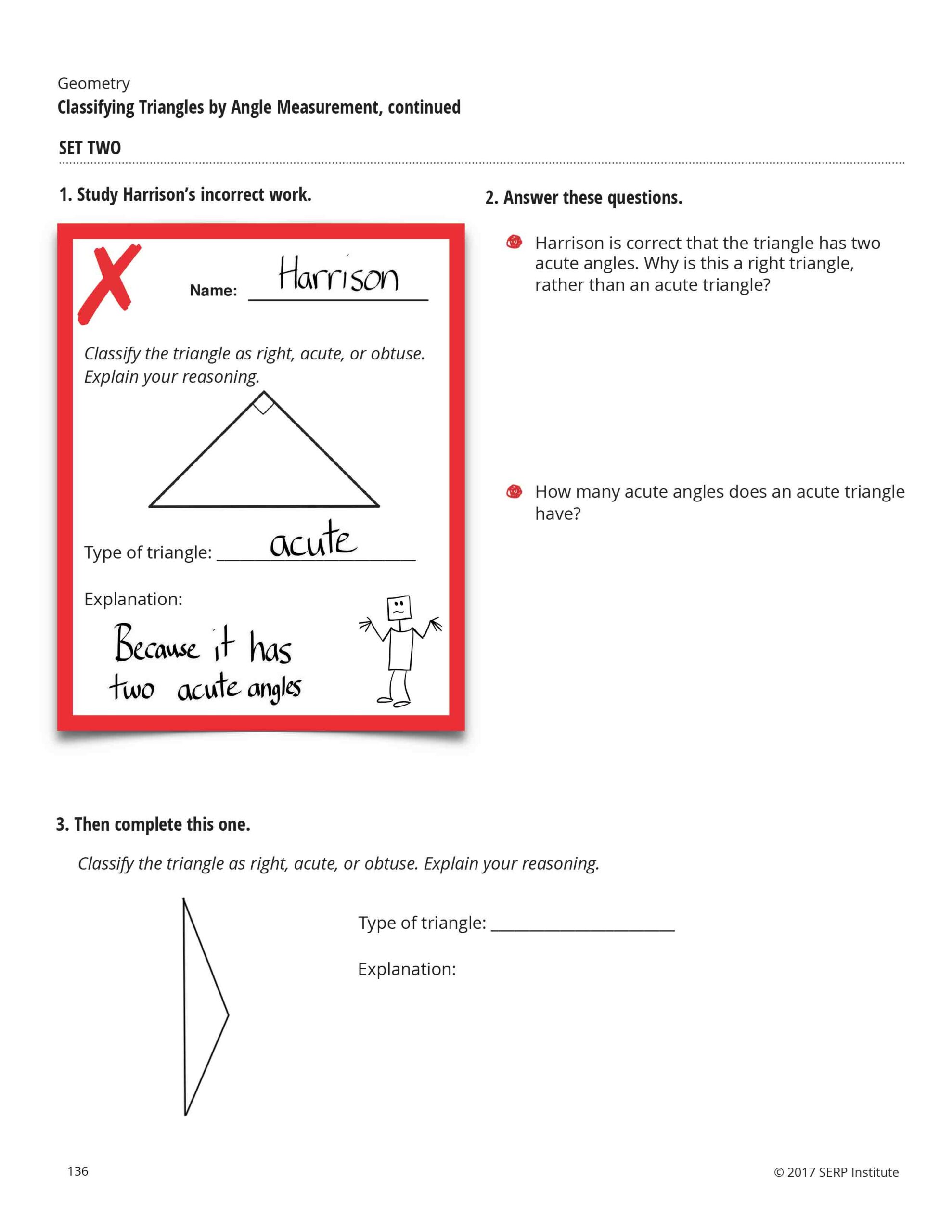
In their “MathByExample” project, students read and analyze one correct and and one incorrect solution for each problem; explain the reasoning behind the solutions and identify misconceptions that led to incorrect solutions; then apply that understanding to similar problems.

The researchers talked with Education Week about how to help students use already-worked problems to learn from their own misconceptions in math.
How do you teach students to think about mistakes?
Julie Booth: The idea is that instead of just solving a whole bunch of practice problems by themselves, half of those problems are replaced with either: a fictitious student solving that problem correctly and giving the real student questions to answer about what’s going on in the fictitious student’s work; or that fictitious student might have gotten it wrong—and it’s clearly marked as wrong—and the real student has to answer questions about what might have been going on and why that fictitious student missed that problem. What did [the fictitious student] not notice in the problem? What kinds of things about their work are demonstrating why it’s a wrong solution? They’re reviewing it and they’re explaining it. They’re not judging it.
Why can’t you just have students judge whether a set of problems are correct or not?
Booth: Some people have tried to use the approach of having the student judge whether it’s correct or incorrect, and that doesn’t work. Struggling students tend to benefit from [studying both correct and incorrect examples], maybe even to a greater level than average or above-average students, but if you just ask them to tell you whether [a problem] is right or wrong, the struggling students don’t know that it’s wrong. Oftentimes they’ll look at it like, ‘yes, that’s how I would’ve done it.’ So [the problem] has to be clearly marked as wrong for them to be able to engage with it and understand that it’s part of the learning process.
How does this approach change the way math instruction looks in the classroom?
Booth: It doesn’t change the pacing; it doesn’t change anything about what [content] teachers get to and what they don’t. Teachers have reported that it changes the quality of the conversations that the students have and their understanding of their own misconceptions.
What are you learning about the kinds of math misconceptions that can persist over time?
Booth: Oftentimes, a misconception is based on a particular way that [a student] learned an earlier concept, and it carries through. Just because they don’t understand how negatives work doesn’t mean that they also don’t understand how the equal sign works. Oftentimes, a particular type of misconception manifests in multiple ways, but it doesn’t necessarily predict that they’ll have another particular type of misconception.
Allie Huyghe: In [high school] geometry, we expected students to come in with a base of grade 3-8 content. So, for example, they may have foundations around basic shapes and stuff, but [have misconceptions around] ‘why is a square a rectangle, but a rectangle isn’t a square’? Even basics as far back as that apply in being able to do any sort of simple quadratic proof.
SOURCE: EDUCATION WEEK